
Calculus, 8th Edition
By Deborah Hughes-Hallett, Andrew M. Gleason, and William G. McCallum, et al.
The Calculus Consortium’s focus on the “Rule of Four” (viewing problems graphically, numerically, symbolically, and verbally) has become an integral part of teaching calculus in a way that promotes critical thinking to reveal solutions to mathematical problems. Their approach reinforces the conceptual understanding necessary to reduce complicated problems to simple procedures without losing sight of the practical value of mathematics. In this edition of Calculus, the authors continue their focus on introducing different perspectives for students with an increased emphasis on active learning in a ‘flipped’ classroom.
The world has evolved, and the Consortium has too; the authors continue their focus on introducing different perspectives for students with an increased emphasis on providing tools for a variety of classroom formats. Algorithmic auto-graded homework questions, videos, active learning worksheets, and many viewable student metrics provide a comprehensive, data-driven approach to engage students. New graphing questions and visual aids powered by GeoGebra allow for complex, multi-part question types that reinforce the Rule of Four to enhance conceptual understanding and visualization.
The 8th edition features a variety of problems with applications from the physical sciences, health, biology, engineering, and economics, allowing for engagement across multiple majors. The Consortium brings Calculus to (real) life with current, relevant examples and a focus on active learning.
Schedule a Demo Request Instructor AccountWant to learn more about WileyPLUS? Click Here
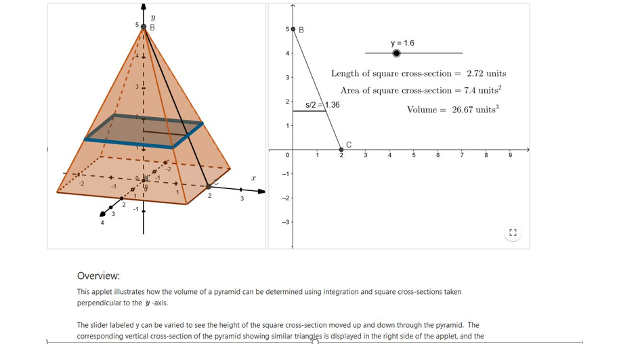
Interactive Explorations
allow visualization of calculus topics and guide students through key concepts for better understanding.

Pre-Lecture and Mini-Lecture Videos with ConcepTests
allow flexibility in any classroom format with author-led discussion on key concepts. These videos provide students with enough information to immediately tackle problems in every section.
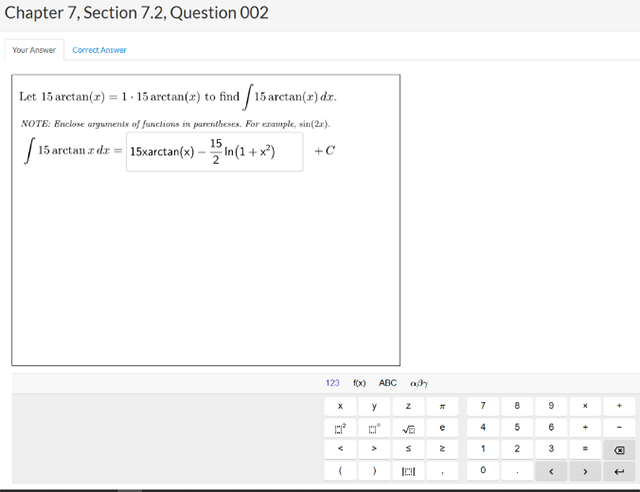
Graphing and Complex Questions Powered by GeoGebra
give instructors the ability to assign more complex auto-graded questions to improve conceptual understanding in math.
Deborah J. Hughes-Hallett is Professor of Mathematics at the University of Arizona. Her expertise is in the undergraduate teaching of mathematics. Hughes-Hallett earned a Bachelor’s Degree in Mathematics from the University of Cambridge in 1966, and a Master’s Degree from Harvard in 1976. She worked as a preceptor and senior preceptor at Harvard from 1975 to 1991, as an instructor at the Middle East Technical University in Ankara, Turkey, from 1981 to 1984, and as a faculty member at Harvard from 1986 to 1998. She served as Professor of the Practice in the teaching of mathematics at Harvard from 1991 to 1998 and continues to hold an affiliation with Harvard as Adjunct Professor of Public Policy in the John F. Kennedy School of Government.
Chapter 1: A Library of Functions
Chapter 2: Key Concept: The Derivative
Chapter 3: Short-Cuts to Differentiation
Chapter 4: Using the Derivative
Chapter 5: Key Concept: The Definite Integral
Chapter 6: Constructing Antiderivatives
Chapter 7: Integration
Chapter 8: Using the Definite Integral
Chapter 9: Sequences and Series
Chapter 10: Approximating Functions
Chapter 11: Differential Equations
Chapter 12: Functions of Several Variables
Chapter 13: A Fundamental Tool: Vectors
Chapter 14: Differentiating Functions of Several Variables
Chapter 15: Optimization: Local and Global Extrema
Chapter 16: Integrating Functions of Several Variables
Chapter 17: Parameterization and Vector Fields
Chapter 18: Line Integrals
Chapter 19: Flux Integrals and Divergence
Chapter 20: The Curl and Stokes’ Theorem
Chapter 21: Parameters, Coordinates, and Integrals

