
Functions Modeling Change, 6th Edition
By Eric Connally
Functions Modeling Change, 6th Edition, now with corequisite support content, combines a modern digital environment with proven pedagogy. It prepares students for calculus by promoting conceptual understanding and the connections among mathematical ideas. The authors emphasize depth of understanding rather than breadth of coverage.
Each function is presented symbolically, numerically, graphically, and verbally (the Rule of Four). Students are encouraged to create mathematical models that relate to the world around them and are exposed to many real-world applications, examples, and problems. WileyPLUS adds algorithmic auto-graded end-of-section questions, including GeoGebra graphing questions to help students visualize and apply mathematical concepts.
Schedule a Demo Request Instructor AccountWant to learn more about WileyPLUS? Click Here
New Corequisite Support Appendices
have been added as a digital appendix to support corequisite courses. The comprehensive coverage of prerequisite topics ranges from prealgebra through intermediate algebra, including step-by-step instructional worksheets that can be used inside or outside of the classroom, and an ample selection of homework and/or quiz exercises for each topic. Utilizing WileyPLUS, you can customize the corequisite topics and truly cater to your individual course needs.
Graphing Questions Powered by GeoGebra
enable real-time manipulations of graphs to boost conceptual understanding utilizing automatic feedback and worked answers. New in WileyPLUS, instructors now can assign more complex auto-graded questions to improve conceptual understanding of math.
WileyPLUS users will have best-in-class math assessment with unique features including:
– Randomization to ensure each student gets a different question
– Automatically marked questions with fully worked solutions
– Assessment of advanced math topics such as differential equations and matrices
Video lectures encourage students to become active learners.
Video Lectures help students come to class better prepared. Mini-lecture videos linked to examples in WileyPLUS provide greater detail to the solution of examples in each section of the text. These may assist students in reading the text prior to class or in reviewing material after class.
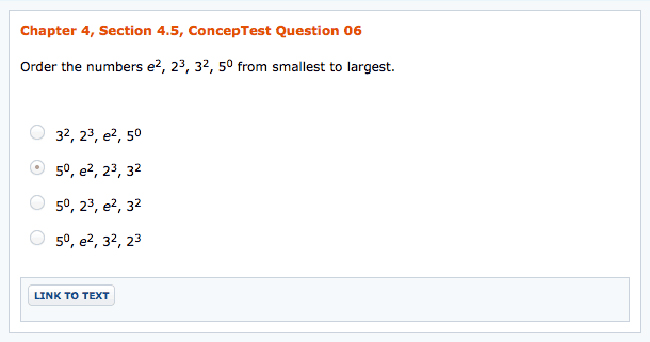
ConcepTest questions help students learn more effectively.
Modeled on the pioneering work of Harvard physicist Eric Mazur, ConcepTest questions are designed to promote active learning during class, particularly (but not exclusively) in large lectures.
- New Corequisite Support Appendices have been added as a digital appendix to support corequisite courses. The comprehensive coverage of prerequisite topics ranges from prealgebra through intermediate algebra, including step-by-step instructional worksheets that can be used inside or outside of the classroom, and an ample selection of homework and/or quiz exercises for each topic.
- Active Learning Worksheets facilitate classroom engagement and enable flipped model and online course implementation. Coupled with the hallmark ConcepTest questions, they provide a solid foundation for supporting an active learning environment.
- 1,350 New Questions: An extensive set of author-developed end-of-section questions have been added to the new 6th Edition course. Over 600 of these are section-level Skill Refresher questions.
- Selected Chapter 9 Topics, such as modeling and sums with different periods, are now digital only and are available through the e-text or WileyPLUS.
- Reorganized Trigonometry Material allows introduction via either triangles or the unit circle. References to circles have been removed from Chapter 8 to focus exclusively on triangle trigonometry.
- The Polar Coordinates section, originally in Chapter 8, now immediately precedes the section on complex numbers in Chapter 9.
- New optional material on the Binomial Theorem and the Fundamental Theorem of Algebra.
What’s New
Eric Connally began his teaching career at Harvard University in 1989, shortly after graduating from Cornell University with a B.A. in Physics in 1988. He joined Wellesley College as coordinator of its Quantitative Reasoning (QR ) Program in 1995. At the time, this innovative program encompassed several new undergraduate degree requirements as well as a course in basic math and data analysis. Together with a colleague who joined the program in 1998, he administered all aspects of the QR program and the associated degree requirements. In 2000, Eric joined a software startup company, Elytics, Inc., as a software engineer.
Eric is now the Director of Engineering, working on a new online math project under development by several members of the Mathematics Consortium Working Group. He continues to teach math at the Harvard Extension School and at the Harvard Kennedy School. He was awarded the International Conference on Technology in Collegiate Mathematics (ICTCM) Award for Excellence and Innovation with the Use of Technology in Collegiate Mathematics and the Petra T. Shattuck Excellence in Teaching Award.
Deborah J. Hughes-Hallett is a mathematician who works as a professor of mathematics at the University of Arizona. Her expertise is in the undergraduate teaching of mathematics. She has also taught as Professor of the Practice in the Teaching of Mathematics at Harvard University, and continues to hold an affiliation with Harvard as Adjunct Professor of Public Policy in the John F. Kennedy School of Government. Hughes-Hallett earned a bachelor’s degree in mathematics from the University of Cambridge in 1966, and a master’s degree from Harvard in 1976. She worked as a preceptor and senior preceptor at Harvard from 1975 to 1991, as an instructor at the Middle East Technical University in Ankara, Turkey from 1981 to 1984, and as a faculty member at Harvard from 1986 to 1998. She served as Professor of the Practice in the Teaching of Mathematics at Harvard from 1991 to 1998. She moved to Arizona in 1998, and took on her adjunct position at the Kennedy School in 2001.
1. Linear Functions and Change
2. Functions
3. Quadratic Functions
4. Exponential Functions
5. Logarithmic Functions
6. Transformations of Functions and Their Graphs
7. Trigonometry and Periodic Functions
8. Triangle Trigonometry and Polar Coordinates
9. Trigonometric Identities, Models, and Complex Numbers
10. Compositions, Inverses, and Combinations of Functions
11. Polynomial and Rational Functions
12. Vectors and Matrices
13. Sequences and Series
14. Parametric Equations and Conic Sections
Appendix: Corequisite Materials (Digital Only)
Answers to Odd Problems
Index

