
Elementary Differential Equations and Boundary Value Problems, 12th Edition
By William E. Boyce, Richard C. DiPrima, and Douglas B. Meade
Elementary Differential Equations and Boundary Value Problems, 12th Edition is written from the viewpoint of the applied mathematician, whose interest in differential equations may sometimes be quite theoretical, sometimes intensely practical, and often somewhere in between. In this revision new author Douglas Meade focuses on developing students conceptual understanding with new Interactive Figures in WileyPLUS that bring concepts to life, along with new concept check questions and worksheets for each chapter.
Elementary Differential Equations and Boundary Value Problems 12th Edition combines sound and accurate (but not abstract) exposition of the elementary theory of differential equations with considerable material on methods of solution, analysis, and approximation that have proved useful in a wide variety of applications.
Schedule a Demo Request Instructor AccountWant to learn more about WileyPLUS? Click Here
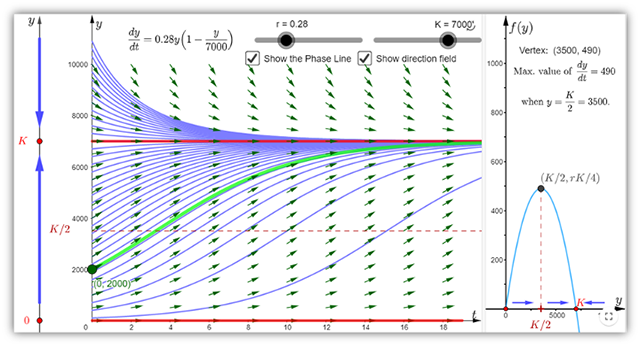
Interactive Figures
Interactive Figures powered by GeoGebra have been created for many of the figures from the text bringing concepts to life. These figures can be found in WileyPLUS and embedded within the e-text. Interactive figures are also utilized in WileyPLUS for evaluation on homework, quizzes, and tests.

Worked Examples Video Series
Worked example video series has been included in WileyPLUS to provide students with clear, accurate, and pedagogically sound videos all in one place.
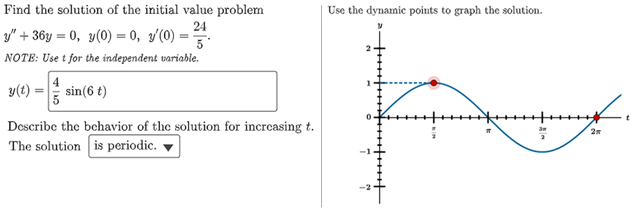
Interactive Questions
Symbolic math and graphing questions powered by GeoGebra allow assignment of more complex auto-graded questions to enhance conceptual understanding.
What’s New to This Course
- Concept Checks have been added to every end of chapter question sets. Concept Check are designed to reinforce key chapter learning objectives and prepare students for the end-of-chapter problems
- Interactive Figures powered by GeoGebra have been created for many of the figures from the text bringing concepts to life. These figures can be found in WileyPLUS and embedded within the e-text. Interactive figures are also utilized in WileyPLUS for evaluation on homework, quizzes, and tests.
- Updated Question Banks now include more exercises from the text available in WileyPLUS than ever before.
- Worksheets have been developed as a lecture aid to teach class in a synchronous in-person, online or hybrid environment. Worksheets are designed to help students follow the presentation and discussion of topics in each section. When completed the students should have a good set of notes with examples for that section.
- New TestGen computerized test bank allows for quick creation of algorithmic quizzes or tests. TestGen provides a variety of question types and also allows instructors to create their own questions.
Additional Features Include
Instructor Resources-
-
- Instructor’s Solutions Manual
- Lecture Note PowerPoints
- Chapter Review Sheets
- Maple Technology Resources
- MATLAB Technology Resources
- Mathematica Technology Resources
- Projects
- WileyPLUS Question Index
- Interactive Figures powered by GeoGebra
- Printed Test Bank
- TestGen Computerized Test Bank
-
-
- Chapter Review Sheets
- Interactive Figures powered by GeoGebra
- Student Solutions Manual
- Maple Technology Resources
- MATLAB Technology Resources
- Mathematica Technology Resources
- Projects
In memory of William Boyce and Richard DiPrima. Two men whose passion for differential equations was instrumental in the shaping of my career. I am forever grateful.

William E. Boyce (deceased) received his B.A. degree in Mathematics from Rhodes College and his M.S. and Ph.D. degrees in Mathematics from Carnegie Mellon University. He was a member of the American Mathematical Society, the Mathematical Association of America, and the Society for Industrial and Applied Mathematics. He was also the Edward P. Hamilton Distinguished Professor Emeritus of Science Education (Department of Mathematical Sciences) at Rensselaer. He authored numerous technical papers in boundary value problems and random differential equations and their applications, as well as several textbooks including two differential equations texts, and was the coauthor (with M.H. Holmes, J.G. Ecker, and W.L. Siegmann) of a text on using Maple to explore Calculus. He was also coauthor (with R.L. Borrelli and C.S. Coleman) of Differential Equations Laboratory Workbook (Wiley 1992), which received the EDUCOM Best Mathematics Curricular Innovation Award in 1993. Professor Boyce was a member of the NSF-sponsored CODEE (Consortium for Ordinary Differential Equations Experiments) that led to the widely acclaimed ODE Architect. He was active in curriculum innovation and reform. Among other things, he was the initiator of the Computers in Calculus project at Rensselaer, partially supported by the NSF. In 1991, he received the William H. Wiley Distinguished Faculty Award given by Rensselaer. Professor Boyce passed away on November 4, 2019.

Richard C. DiPrima (deceased) (deceased) received his B.S., M.S., and Ph.D. degrees in Mathematics from Carnegie-Mellon University. He joined the faculty of Rensselaer Polytechnic Institute after holding research positions at MIT, Harvard, and Hughes Aircraft. He held the Eliza Ricketts Foundation Professorship of Mathematics at Rensselaer, was a fellow of the American Society of Mechanical Engineers, the American Academy of Mechanics, and the American Physical Society. He was also a member of the American Mathematical Society, the Mathematical Association of America, and the Society for Industrial and Applied Mathematics. He served as the Chairman of the Department of Mathematical Sciences at Rensselaer, as President of the Society for Industrial and Applied Mathematics, and as Chairman of the Executive Committee of the Applied Mechanics Division of ASME. In 1980, he was the recipient of the William H. Wiley Distinguished Faculty Award given by Rensselaer. He received Fulbright fellowships in 1964-65 and 1983 and a Guggenheim fellowship in 1982-83. He was the author of numerous technical papers in hydrodynamic stability and lubrication theory and two texts on differential equations and boundary value problems. Professor DiPrima passed away on September 10, 1984.
Douglas B. Meade received B.S. degrees in Mathematics and Computer Science from Bowling Green State University, an M.S. in Applied Mathematics from Carnegie Mellon University, and a Ph.D. in mathematics from Carnegie Mellon University. After a two-year stint at Purdue University, he joined the mathematics faculty at the University of South Carolina, where he is currently an Associate Professor of mathematics. He is a member of the American Mathematical Society, Mathematics Association of America, and Society for Industrial and Applied Mathematics; in 2016 he was named an ICTCM Fellow at the International Conference on Technology in Collegiate Mathematics (ICTCM). His primary research interests are in the numerical solution of partial differential equations arising from wave propagation problems in unbounded domains and from population models for infectious diseases. He is also well-known for his educational uses of computer algebra systems, particularly Maple. These include Getting Started with Maple (with M. May, C-K. Cheung, and G. E. Keough, Wiley, 2009, ISBN 978-0- 470-45554-8), Engineer’s Toolkit: Maple for Engineers (with E. Bourkoff, Addison-Wesley, 1998, ISBN 0-8053-6445-5), and numerous Maple supplements for numerous calculus, linear algebra, and differential equations textbooks – including previous editions of this book. He was a member of the MathDL New Collections Working Group for Single Variable Calculus and chaired the Working Groups for Differential Equations and Linear Algebra.
Chapter 1: Introduction
Chapter 2: First-Order Differential Equations
Chapter 3: Second-Order Linear Equations
Chapter 4: Higher-Order Linear Equations
Chapter 5: Series Solutions of Second-Order Linear Equations
Chapter 6: The Laplace Transform
Chapter 7: Systems of First-Order Linear Equations
Chapter 8: Numerical Methods
Chapter 9: Nonlinear Differential Equations and Stability
Chapter 10: Partial Differential Equations and Fourier Series
Chapter 11: Boundary Value Problems and Sturm-Liouville Theory

