
Calculus: Early Transcendentals, 12th Edition
By Howard Anton, Irl C. Bivens, Stephen Davis
Anton’s Calculus encourages student comprehension through a balance between clarity of explanations and mathematical rigor. WileyPLUS for Anton’s Calculus combines a modern digital environment that is flexible and customizable. WileyPLUS gives you control to shape your calculus course to engage and motivate students. New symbolic palette and graphing questions powered by GeoGebra allow assigning more complex auto-graded graphing and symbolic notation questions to enhance conceptual understanding in math. Detailed mathematical explanations are augmented by varied online exercises, applications, and real-life examples. Built-in trigonometry refresher materials are also available to help support under-prepared students.
Schedule a Demo Request Instructor AccountWant to learn more about WileyPLUS? Click Here
Example Videos
Videos of worked examples and problems cover the subject material in the single variable sections of the course now available with integrated assessment questions to keep students engaged in the material.
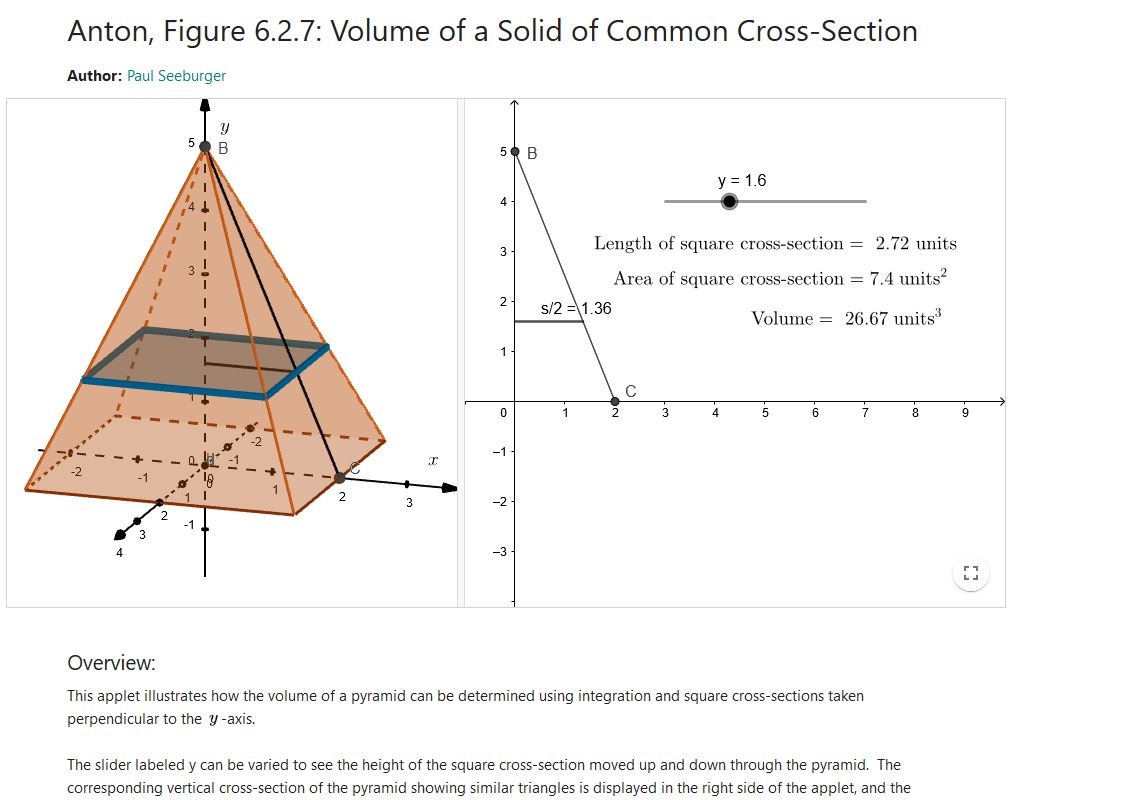
Interactive Animations
Interactive figures powered by GeoGebra allow visualization of calculus topics and guide students through key concepts for better understanding.
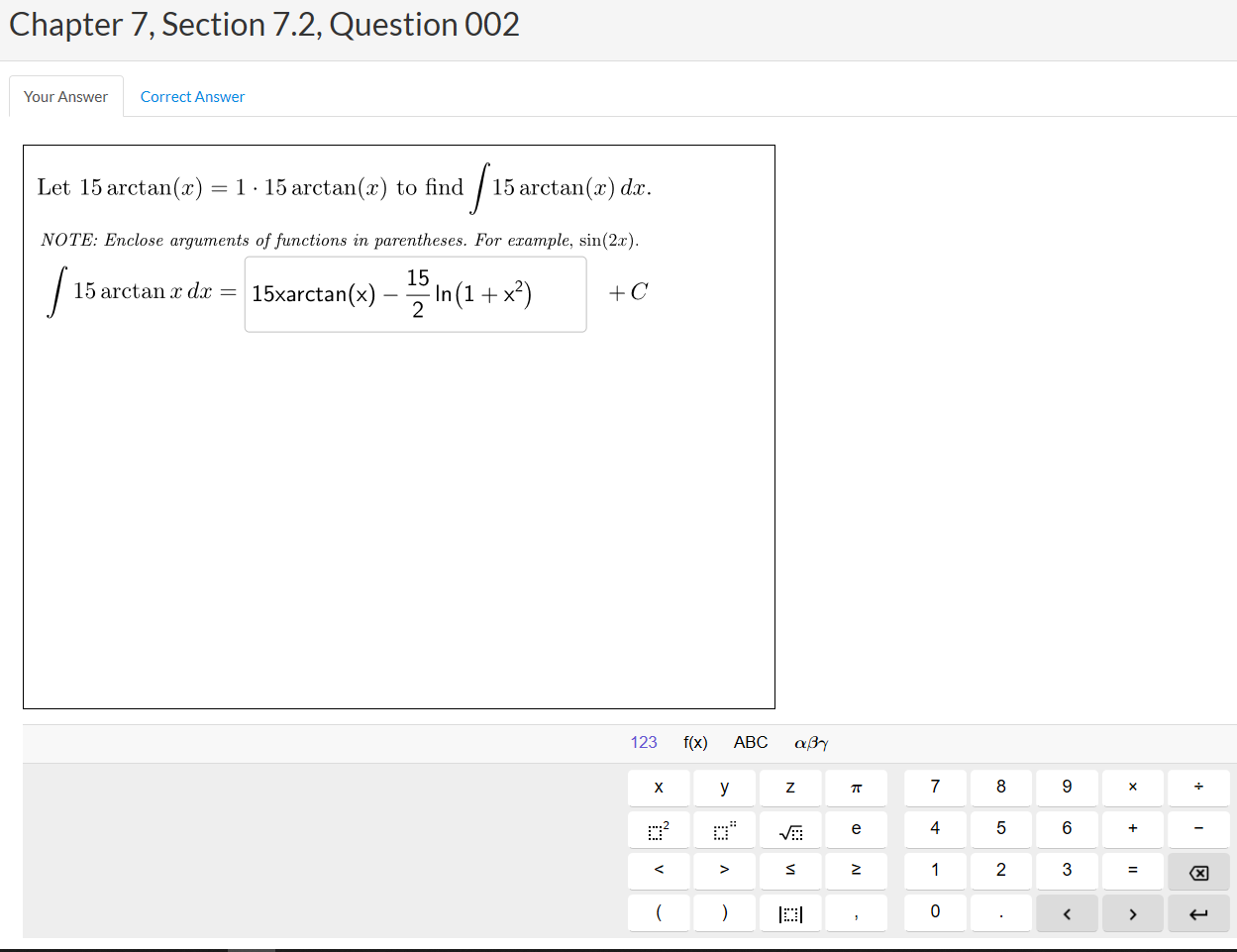
New Interactive Questions
Symbolic and graphing questions powered by GeoGebra give instructors the ability to assign more complex auto-graded questions to enhance conceptual understanding in math.
What’s New
- New proof problems: Assignable and automatically-graded proof problems help students build confidence and understand the entire process of writing proofs as they get practice and immediate feedback.
- Example Videos now with Assignable Questions: Videos of worked examples and problems cover the subject material in the single variable sections of the course now available with integrated assessment questions to keep students engaged in the material.
- New Interactive Questions: Symbolic palette and graphing questions powered by GeoGebra give instructors the ability to assign more complex auto-graded questions to enhance conceptual understanding in math.
- Test Bank Questions: Algorithmic test bank questions have been added to the WileyPLUS question bank.
- New TestGen computerized test bank allows for quick creation of algorithmic quizzes or tests. TestGen provides a variety of question types and also allows instructors to create their own questions.

Howard Anton obtained his B.A. from Lehigh University, his M.A. from the University of Illinois, and his Ph.D. from the Polytechnic University of Brooklyn, all in mathematics. In the early 1960s he worked for Burroughs Corporation and Avco Corporation at Cape Canaveral, Florida, where he was involved with the manned space program. In 1968 he joined the Mathematics Department at Drexel University, where he taught full time until 1983. Since that time he has been an Emeritus Professor at Drexel and has devoted most of his time to textbook writing and activities for mathematical associations. Dr. Anton was president of the EPADEL section of the Mathematical Association of America (MAA), served on the Board of Governors of that organization, and guided the creation of the student chapters of the MAA. He has published numerous research papers in functional analysis, approximation theory, and topology, as well as pedagogical papers. He is best known for his textbooks in linear algebra and calculus, which are among the most widely used in the world. There are currently more than one hundred versions of his books, including translations into Spanish, Arabic, Portuguese, Italian, Indonesian, French, Japanese, Chinese, Hebrew, and German. His textbook in linear algebra has won both the Textbook Excellence Award and the McGuffey Award from the Textbook Author’s Association. For relaxation, Dr. Anton enjoys traveling and photography.
Irl C. Bivens received his A.B. from Pfeiffer College and his Ph.D. from the University of North Carolina at Chapel Hill, both in mathematics. After positions at Pfeiffer College and Rice University, he joined the Department of Mathematics at Davidson College in 1982. At Davidson, he was privileged to teach courses in analysis, geometry, the history of mathematics, and recreational mathematics until his retirement as Emeritus Professor in 2018. Professor Bivens has published numerous articles on undergraduate mathematics and is a recipient of the George Polya Award, the Merten M. Hasse Prize for Expository Writing in Mathematics, and, together with Benjamin G. Klein, the Carl B. Allendoerfer Award. Past service to the MAA includes membership on the editorial boards of The College Mathematics Journal, the Problem Book series, and Dolciani Mathematical Expositions, as well as service on MAA awards committees for expository writing. For recreation, he enjoys swimming, juggling, reading, and mathematical magic.
Stephen L. Davis received his B.A. from Lindenwood College and his Ph.D. from Rutgers University in mathematics. Having previously taught at Rutgers University and the Ohio State University, Dr. Davis joined the faculty at Davidson College in 1981, teaching courses that included calculus, linear algebra, abstract algebra, and computer science, until retiring as Emeritus Professor in 2019. Professor Davis held several offices in the Southeastern section of the MAA, including chair and secretary-treasurer, and represented the section on the MAA Board of Governors. He has been involved at all levels in the grading of the Advanced Placement® Calculus Exam starting in 1988, served as Chief Reader during 2015—2019, and has been a member and chair of the AP® Calculus Development Committee. Locally, he continues to be actively involved in nurturing mathematically talented middle and high school students through leadership in the Charlotte Mathematics Club. Professor Davis and his wife Elisabeth enjoy traveling and time with family. They have three children, Laura, Anne, and James, all former calculus students.
-
- LIMITS AND CONTINUITY
- 1.1 Limits (An Intuitive Approach)
- 1.2 Computing Limits
- 1.3 Limits at Infinity; End Behavior of a Function
- 1.4 Limits (Discussed More Rigorously)
- 1.5 Continuity
- 1.6 Continuity of Trigonometric Functions
- 1.7 Inverse Trigonometric Functions
- 1.8 Exponential and Logarithmic Functions
- THE DERIVATIVE
- 2.1 Tangent Lines and Rates of Change
- 2.2 The Derivative Function
- 2.3 Introduction to Techniques of Differentiation
- 2.4 The Product and Quotient Rules
- 2.5 Derivatives of Trigonometric Functions
- 2.6 The Chain Rule
- TOPICS IN DIFFERENTIATION
- 3.1 Implicit Differentiation
- 3.2 Derivatives of Logarithmic Functions
- 3.3 Derivatives of Exponential and Inverse Trigonometric Functions
- 3.4 Related Rates
- 3.5 Local Linear Approximation; Differentials
- 3.6 L’Hôpital’s Rule; Indeterminate Forms
- THE DERIVATIVE IN GRAPHING AND APPLICATIONS
- 4.1 Analysis of Functions I: Increase, Decrease, and Concavity
- 4.2 Analysis of Functions II: Relative Extrema; Graphing Polynomials
- 4.3 Analysis of Functions III: Rational Functions, Cusps, and Vertical Tangents
- 4.4 Absolute Maxima and Minima
- 4.5 Applied Maximum and Minimum Problems
- 4.7 Newton’s Method
- 4.8 Rolle’s Theorem; Mean-Value Theorem
- INTEGRATION
- 5.1 An Overview of the Area Problem
- 5.2 The Indefinite Integral
- 5.3 Integration by Substitution
- 5.4 The Definition of Area as a Limit; Sigma Notation
- 5.5 The Definite Integral
- 5.6 The Fundamental Theorem of Calculus
- 5.7 Rectilinear Motion Revisited Using Integration
- 5.8 Average Value of a Function and its Applications
- 5.9 Evaluating Definite Integrals by Substitution
- 5.10 Logarithmic and Other Functions Defined by Integrals
- APPLICATIONS OF THE DEFINITE INTEGRAL IN GEOMETRY, SCIENCE, AND ENGINEERING
- 6.1 Area Between Two Curves
- 6.2 Volumes by Slicing; Disks and Washers
- 6.3 Volumes by Cylindrical Shells
- 6.4 Length of a Plane Curve
- 6.5 Area of a Surface of Revolution
- 6.6 Work
- 6.7 Moments, Centers of Gravity, and Centroids
- 6.8 Fluid Pressure and Force
- 6.9 Hyperbolic Functions and Hanging Cables
- PRINCIPLES OF INTEGRAL EVALUATION
- 7.1 An Overview of Integration Methods
- 7.2 Integration by Parts
- 7.3 Integrating Trigonometric Functions
- 7.4 Trigonometric Substitutions
- 7.5 Integrating Rational Functions by Partial Fractions
- 7.6 Using Computer Algebra Systems and Tables of Integrals
- 7.7 Numerical Integration; Simpson’s Rule
- 7.8 Improper Integrals
- MATHEMATICAL MODELING WITH DIFFERENTIAL EQUATIONS
- 8.1 Modeling with Differential Equations
- 8.2 Separation of Variables
- 8.3 Slope Fields; Euler’s Method
- 8.4 First-Order Differential Equations and Applications
- INFINITE SERIES
- 9.1 Sequences
- 9.2 Monotone Sequences
- 9.3 Infinite Series
- 9.4 Convergence Tests
- 9.5 The Comparison, Ratio, and Root Tests
- 9.6 Alternating Series; Absolute and Conditional Convergence
- 9.7 Maclaurin and Taylor Polynomials
- 9.8 Maclaurin and Taylor Series; Power Series
- 9.9 Convergence of Taylor Series
- 9.10 Differentiating and Integrating Power Series; Modeling with Taylor Series
- PARAMETRIC AND POLAR CURVES; CONIC SECTIONS
- 10.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves
- 10.2 Polar Coordinates
- 10.3 Tangent Lines, Arc Length, and Area for Polar Curves
- 10.4 Conic Sections
- 10.5 Rotation of Axes; Second-Degree Equations
- 10.6 Conic Sections in Polar Coordinates
- THREE-DIMENSIONAL SPACE; VECTORS
- 11.1 Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces
- 11.2 Vectors
- 11.3 Dot Product; Projections
- 11.4 Cross Product
- 11.5 Parametric Equations of Lines
- 11.6 Planes in 3-Space
- 11.7 Quadric Surfaces
- 11.8 Cylindrical and Spherical Coordinates
- VECTOR-VALUED FUNCTIONS
- 12.1 Introduction to Vector-Valued Functions
- 12.2 Calculus of Vector-Valued Functions
- 12.3 Change of Parameter; Arc Length
- 12.4 Unit Tangent, Normal, and Binormal Vectors
- 12.5 Curvature
- 12.6 Motion Along a Curve
- 12.7 Kepler’s Laws of Planetary Motion
- PARTIAL DERIVATIVES
- 13.1 Functions of Two or More Variables
- 13.2 Limits and Continuity
- 13.3 Partial Derivatives
- 13.4 Differentiability, Differentials, and Local Linearity
- 13.5 The Chain Rule
- 13.6 Directional Derivatives and Gradients
- 13.7 Tangent Planes and Normal Vectors
- 13.8 Maxima and Minima of Functions of Two Variables
- 13.9 Lagrange Multipliers
- MULTIPLE INTEGRALS
- 14.1 Double Integrals
- 14.2 Double Integrals over Nonrectangular Regions
- 14.3 Double Integrals in Polar Coordinates
- 14.4 Surface Area; Parametric Surfaces
- 14.5 Triple Integrals
- 14.6 Triple Integrals in Cylindrical and Spherical Coordinates
- 14.7 Change of Variables in Multiple Integrals; Jacobians
- 14.8 Centers of Gravity Using Multiple Integrals
- TOPICS IN VECTOR CALCULUS
- 15.1 Vector Fields
- 15.2 Line Integrals
- 15.3 Independence of Path; Conservative Vector Fields
- 15.4 Green’s Theorem
- 15.5 Surface Integrals
- 15.6 Applications of Surface Integrals; Flux
- 15.7 The Divergence Theorem
- 15.8 Stokes’ Theorem
- LIMITS AND CONTINUITY
- APPENDICES
- A Trigonometry Review (Summary)
- B Functions (Summary)
- C New Functions From Old (Summary)
- D Families of Functions (Summary)
- E Inverse Functions (Summary)
- INDEX
- WEB APPENDICES (online only)
- A Trigonometry Review
- B Functions
- C New Functions From Old
- D Families of Functions
- E Inverse Functions
- F Real Numbers, Intervals, and Inequalities
- G Absolute Value
- H Coordinate Planes, Lines, and Linear Functions
- I Distance, Circles, and Quadratic Equations
- J Solving Polynomial Equations
- K Graphing Functions Using Calculators and Computer Algebra Systems
- L Selected Proofs
- M Early Parametric Equations Option
- N Mathematical Models
- O The Discriminant
- P Second-Order Linear Homogeneous Differential Equations

