
Advanced Engineering Mathematics, 10th Edition
By Erwin Kreyszig
Advanced Engineering Mathematics is known for its comprehensive coverage, careful and correct mathematics, outstanding exercises, and self-contained subject matter parts for maximum flexibility. This course provides students with comprehensive and up-to-date resources for learning engineering mathematics for engineers and physicists, mathematicians and computer scientists, as well as members of other disciplines.
Schedule a Demo Request Instructor AccountWant to learn more about WileyPLUS? Click Here

Worked Example Videos
Worked example videos help build problem-solving skills, providing students with the opportunity to see and hear relevant examples as they are being explained and solved in detail.

Solutions Manual and Study Guide
Selected solutions and practice assignments with hints and help are integrated into WileyPLUS, facilitating independent study and enabling students to immediately check their work.
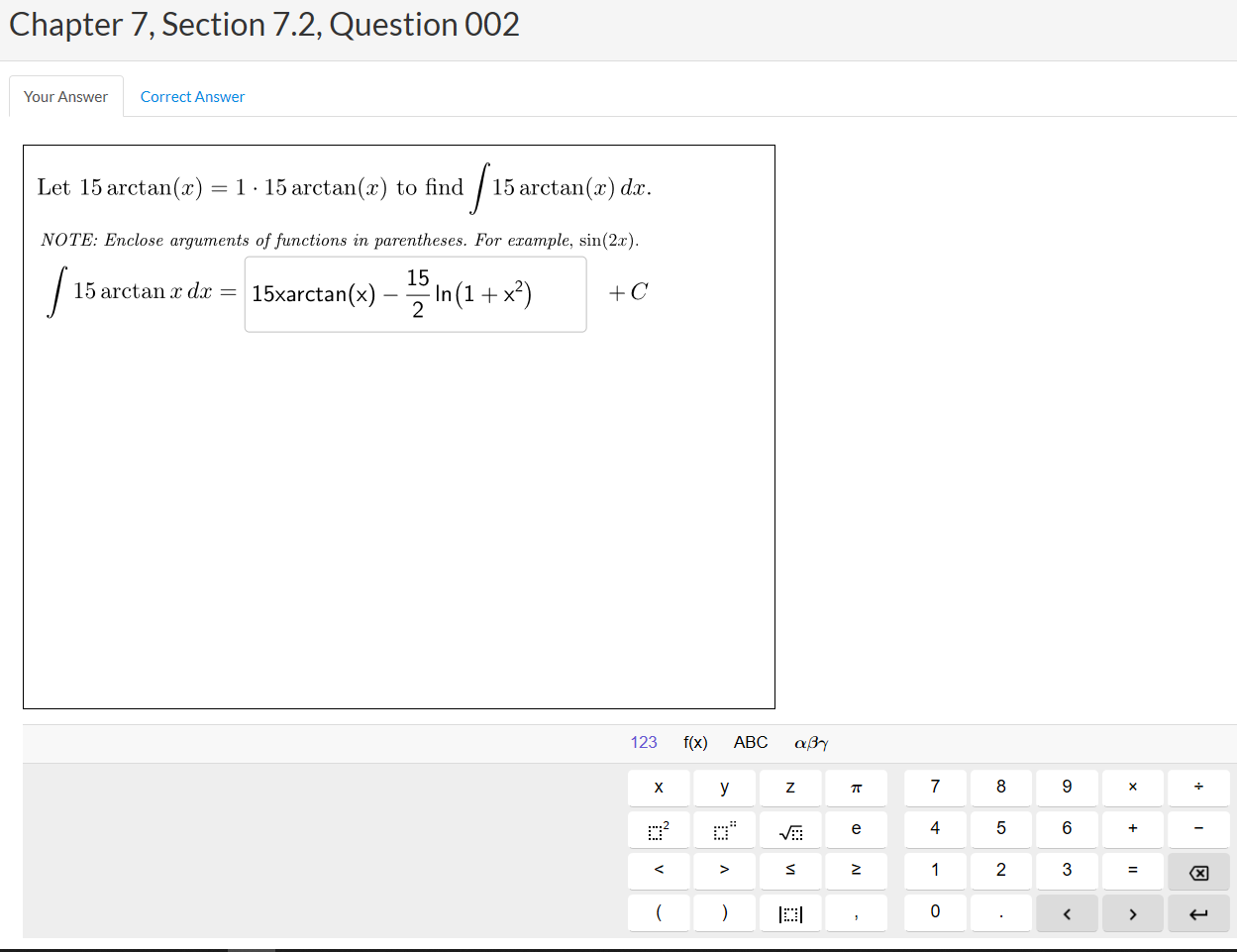
New Interactive Questions
New in WileyPLUS, symbolic palette and graphing questions powered by GeoGebra give instructors the ability to assign more complex auto-graded questions to enhance conceptual understanding in math. Enhance your homework assessments with flexible, accurate, and reliable symbolic palette entry and real-time manipulation of graphs.
Chapter 1. First-Order ODEs
Chapter 2. Second-Order Linear ODEs
Chapter 3. Higher Order Linear ODEs
Chapter 4. Systems of ODEs. Phase Plane. Qualitative Methods
Chapter 5. Series Solutions of ODEs. Special Functions
Chapter 6. Laplace Transforms
Chapter 7. Linear Algebra: Matrices, Vectors, Determinants. Linear Systems
Chapter 8. Linear Algebra: Matrix Eigenvalue Problems
Chapter 9. Vector Differential Calculus. Grad, Div, Curl
Chapter 10. Vector Integral Calculus. Integral Theorems
Chapter 11. Fourier Analysis
Chapter 12. Partial Differential Equations (PDEs)
Chapter 13. Complex Numbers and Functions. Complex Differentiation
Chapter 14. Complex Integration
Chapter 15. Power Series, Taylor Series
Chapter 16. Laurent Series. Residue Integration
Chapter 17. Conformal Mapping
Chapter 19. Numerics in General
Chapter 20. Numeric Linear Algebra
Chapter 21. Numerics for ODEs and PDEs
Chapter 22. Unconstrained Optimization. Linear Programming
Chapter 23. Graphs. Combinatorial Optimization
Chapter 24. Data Analysis. Probability Theory
Chapter 25. Mathematical Statistics
A. References
B. Answers to Odd-Numbered Problems
C. Auxiliary Material
D. Additional Proofs
E. Tables
Index
Photo Credits

